Audio CDs (3) of the Real Estate Principles Textbook - $29.95 may be purchased through the American Schools ONLINE Catalog at: http://americanschoolsonline.com Listen to sample audios at: http://americanschoolsonline.com/audio
SHORT
INTRODUCTION TO CALIFORNIA REAL ESTATE PRINCIPLES,
© 1994 by Home Study, Inc. dba American Schools
Click on link to go to:
Table of Contents; Chapter I: Real Property; Chapter II: Legal Ownership; Chapter III: Agency & Ethics; Chapter IV: Contracts; Chapter V: Real Estate Mathematics; Chapter VI: Financing; Chapter VII: Mortgage Insurance; Chapter VIII: Appraisal; Chapter IX: Transfers of Real Estate; Chapter X: Property Management; Chapter XI: Land Control; Chapter XII: Taxation; Chapter XIII: Fair Housing Laws; Chapter XIV: Macroeconomics; Chapter XV: Legal Professional Requirements; Chapter XVI: Notarial Law; Chapter XVII: Selling Real Estate; Chapter XVIII: Trust Funds Handling; Glossary; Index.
Chapter V: Real Estate
Mathematics
Educational Objectives:
Learn about Interest Computation and Tables,
Three-Variable Formulas, Prorations,
R. E. TERMS GLOSSARY, INDEX.
(The following is reprinted by permission
from the CalBRE Reference Book, p. 263-269, 783-792)
The practice of real estate requires almost
daily calculations of mortgage interest and principal, monthly payments,
prorations, square footage, yields and similar basic math computations.
Although most computations today are done with computers through the use of
specially designed software programs or with a hand-held calculator/computer
while using convenient charts showing needed tables and formulas, the real
estate licensee should know how to solve common problems relating to real
estate without benefit of a calculator, since he or she may encounter
situations requiring math solutions when no electronic assistance is available.
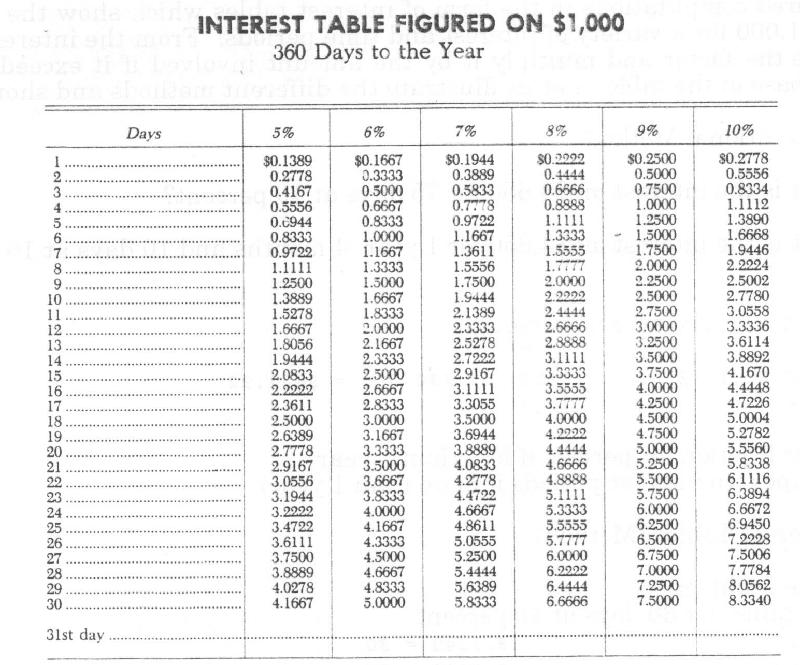
INTEREST COMPUTATION
AND TABLES
Simple interest
computation involves multiplying the principal (amount of note) by the selected
interest rate and the product or result is the interest for one year. Remember,
the interest rate (.06 or .09 for example) is a decimal and two points are to
be marked off from the right.
There are 12 months in a year or 365 days. This
latter figure makes for an awkward denominator. As a result, as an acceptable
business practice, we assume 12 months of 30 days each, or 360 days to a year.
To avoid long computations which may involve
cumbersome fractions, it is common to use prepared computations in the form of
interest tables which show the base as $1, $100 or $1,000 for a variety of
interest and time periods. From the interest table, we determine the factor and
multiply it by the amount involved if it exceeds or is less than the base of
the table. Let us illustrate the different methods and short cuts:
Long Conventional Method
a. What is the interest on $4,650 for 75 days at
10 percent?
b. What is the interest on $4,650 for 1
year, 4 months and 10 days at 10 percent?
Answer:
(a) 4650 X .10 X 75/360 = $96.88
|360|
(b)
4650 X .10 X |120|
or 490/360 = $632.92
|
10|
(Proper fraction for periods if less than 1 year)
(Improper fraction for periods if more than 1
year)
Use of Interest Tables (Method)
(a) Same problem
Look in table for 30 days at 10 percent
factor is 8.3340
= 30
factor is 8.3340
= 80
factor for 15
days 4.1670
= 15
20.835075
days
$4,650 = $4.65 per
$1,000
Multiply
$4.65 X 20.8350
= $96.88
(b) Table not complete
to show higher factors, but it could be done this way:
30 day factor 8.3340
X16 (16 months)
133.3440
+
2.7780
(10 days)
136.1220
factor for 1 year, 4 months and 10 days at $1,000
136.1220
X4.65
(to get additional thousands)
632.92 Answer
OTHER SHORTCUT METHODS FOR COMPUTING SIMPLE
INTEREST
4%: Multiply the principal by number of
days; cut off right- hand figure and divide by 9.
5%: Multiply by number of days and divide
by 72.
6%: Multiply
by number of days; cut off right-hand figure and divide by 6.
7%: Compile the interest for 6% and add
1/6.
8%: Multiply by number of days and divide
by 45.
9%: Multiply
by number of days; cut off right-hand figure and divide by 4.
10%: Multiply by number of days and
divide by 36.
Bankers 12%-30 day/6%-60 day interest
computation method (Using 360 day
year). To find interest on any principal
amount for 30 days at 12%, or for 60 days
at 6%, simply move the decimal point in
the principal amount two places to left.
What is the interest amount on $8432.67
at 12% for 30 days?
Answer: $84.33
What is the interest amount on $8432.67
at 6% for 60 days?
Answer: $84.33
(Since 12% per annum is 1% a month, and
1% of any number is the hundredth
part of it, then by pointing off two
places from the right of a number, it is in effect divided by 100.)
What is the interest on $7,397.64 at 9%
for 69 days?
Interest @ 6% for 60 days = $73.98
(move decimal two
places to left)
Interest @ 3%
for 60 days = $36.99
(1/2 of 6% amount)
Interest @ 9% for 60
days = $110.97
We still need 9 days
more interest; so
6 days = 1/10 of 60 days 6 days =$11.09
(1/10 of $110.97)
3 days = 1/2 of 6 days 3
days = $5.55
(1/2 of $11.09)
Interest @ 9% for 69
days=$127.61
SOME
HANDY FORMULAS
In three-variable formulas, one variable is
equal to the other two. Place one variable in the top half of an imaginary
circle. Place each of the other two variables in adjacent quarters in the
bottom half of the circle. Divide the circle horizontally by a diameter line.
This is a division line (/).Divide the bottom quarters of the circle vertically
by a radius line. This is a multiplication line ( X ). To find the unknown
variable, cover with finger the unknown variable and complete the calculation.
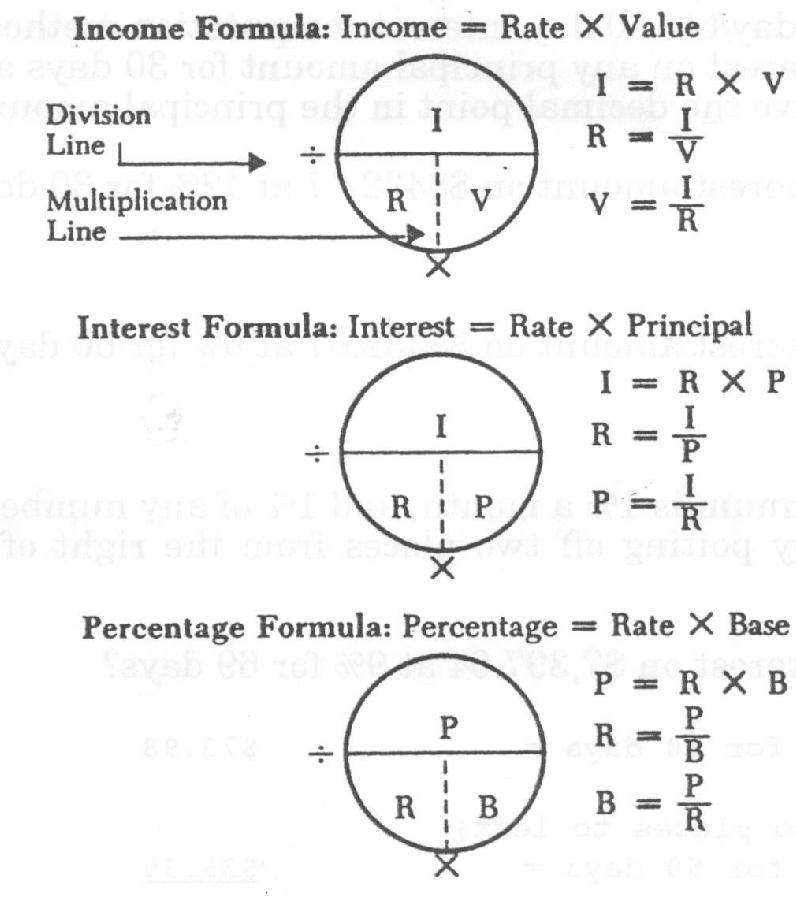
Other three-variable formulas:
Area = Length X Width (A = L X W)
Tax = Assessed Value X Rate (T = A X R)
Commission = Sales Price X Rate (C = S X R)
LINEAR AND SPATIAL MEASUREMENTS AS USED
IN APPRAISING AND LAND DESCRIPTIONS
Common Linear Measurements
One yard = 3
feet or 36 inches. One rod = 16 1/2 feet, 5 1/2yards
One furlong = 40 rods
100 feet = 6.6 rods
One mile = 5,280 feet, 1,760 yards, 320
rods, 80 chains
Surveyors' Measurements
1 link = 7.92 inches;1 rod = 25 links;1
chain = 4 rods, or 66feet.
(These are the old surveyors' measurements.
Modern surveyors use a steel tape or what is called an engineer's chain which
is 100 feet long with links of one foot. Thus, a mile measured by a modern
steel tape chain is 52.8 chains.)
Spatial or Area Measurements (Length X Width)
1 square foot = 144 square inches
1 square yard = 9 square feet
1 square rod = 30 1/4 square yards
1 acre = 10 square chains, 160 square
rods, 4,840 square yards,43,560 square feet
(An acre is an odd and inconsistent measurement.
It is supposed to have been the amount of land that a farmer could plow in a
day with oxen and the old wooden plow. As a square, it is approximately 208.71
feet on a side.)
A section = 1 square
mile, 640 acres
A quarter section = 160 acres
Area of a square or rectangle = length X width
in unit of linear measurement used
Area of a triangle = base X 1/2 altitude
Cubic Measurements (Length X Width X Height)
1 cubic foot = 1,728 cubic inches
1 cubic yard = 27 cubic feet
SOME METRIC EQUIVALENTS
LENGTHS
one foot = 0.3048 meter
one yard = 0.9144 meter
one mile = 1.6093 kilometers or 1609 meters
one meter = 39 inches one kilometer = 3281 feet
or .62 miles or 1000 meters
AREAS
one square foot = 0.0929 Sq. meter
one square yard = 0.836 sq. meter
one acre = 4068.8 sq. meters
one square mile = 259 hectares or 2.59 sq. km.
one square meter = 10.76 sq. feet
one hectare = 2.47
acres or 10,000 sq. meters
Principal -Interest - Rate ?Time
Principal is the amount of money on which
interest is paid usually the loan amount. In a sense, interest is the
"rent" paid by a borrower of money to a lender of money for the use
of the money. It is the cost of borrowing money. Interest is term ed
"simple or "compound.” Simple interest is interest paid only on the
principal owed; compound interest is interest paid on accrued interest as well
as on the principal owed.
The basic simple interest formula used in
finance has four components: interest, principal, rate and time.
I = P X R x T or I = PRT
1.Interest (cost of borrowing
expressed in dollars money paid for the use of money).
2. Principal
(amount of the loan in dollars on which the interest is paid).
3. Rate
(cost of borrowing expressed as a percentage of the principal paid in
interest for one year).
4. Time
(length of time of the loan usually expressed in years).
One must know what three of these four
components are in order to compute the fourth (and unknown) component.
1. Interest
Unknown - Interest = Principal x Rate x Time or I = PRT.
Example: Find the interest on $2500 for 7
years at 13%.
I = PRT
I = $2500 x . 13 x 7
I = $325 X 7
I = $2275
2. Principal
Unknown - Principal = Interest divided by Rate x Time
or
P = I/RxT.
Example: How much money must
be loaned to receive $2275 interest at 13% if the money is loaned for 7 years?
a.
P=I/RT c.P
= $2275/.91
b.
P=$2275/.13x7 d.P
= $2500
3.Rate Unknown Rate = Interest divided by
Principal X Time
or R=I/P X T.
Example: In seven years $2500 earns $2275
interest. What is the rate of interest?
a.
R=I/PT c.
R=$2275/$17,500
b.
R=$2275/$2500x7d. R=.13 or 13%
4. Time Unknown - Time = Interest divided
by Rate x Principal or
T=I/RxP
Example: How long
will it take $2500 to return $2275 interest at an annual rate of 13%?
a.
T=I/PR c.
T=$2275/$325
b.
T=$2275/$2500x.13 d.
T=7 years
Compound interest is more common in advanced
real estate subjects, such as appraisal and annuities. Compound interest tables
are readily available but the principle is discussed here.
As previously stated, compound interest is
interest on the total of the principal and its accrued interest. For each time
period, called the conversion period, interest is added to the principal to
form a new principal amount and each succeeding time period has an increased
principal amount on which to compute interest. Conversion periods may be
monthly, quarterly, semi-annual or annual.
The compound interest rate is usually an annual
rate and must be changed to "interest rate per conversion period" or
"periodic interest rate. " To find compound interest (interest on
interest) the formula for simple interest of I = PRT is used but the symbol
"i" is used instead of RT, "i" being the annual interest
rate divided by the conversion periods per year; so I = Pi.
Example: A $5000 investment at 12% interest
compounded annually for 3 years earns how much interest at maturity? Solution :
Using I = Pi
I = $5,000 X (.12/1)
First year's I =
$5,000 X . 12 or $600.Add to $5000 principal.
Second year's I =
$5,600 x .12 or $672.Add to $5,600 principal.
Third year's I =
$6,272 X . 12 or $752.64.Add to $6,272 principal.
At maturity borrower will owe
$7,024.64.Loan has earned interest of $2,024.64 in 3 years.
Example: How much interest will a $1,000
investment earn over 2 years at 16% interest compounded semi-annually? Solution:
Since the conversion period is semi-annual, the interest rate is computed every
6 months. The periodic interest rate is 16% divided by two conversion periods:
i = 8% for the calculation: I = Pi
1.Original principal amount$1,000.00
2.Interest for 1st period
($1,000X.08) 80.00
3.Balance beginning 2nd period1,080.00
4.Interest earned for 2nd period ($1,080
X .08) 86.40
5.Balance beginning 3rd period1,166.40
6. Interest for 3rd period ($1,166.40 X
.08)93.31
7. Balance beginning last period1,259.71
8. Interest for last period ($1,259.71 x
.08)100.78
9.Compound principal balance1,360.49
I
for 2 years = $1,360.49 - $1,000 or $360.49.
The same problem using annual simple
interest results in $40.49 less interest for the lender ($1,000 X .16 X 2) =
$320 simple interest.
Obviously no one in actual practice is
going to go through the tedious process outlined above to calculate compound
interest. Instead standardized compound interest tables will be used to give
the answer quickly.
The exact formula for computing compound
interest is:
S
= P (1 + i)n
S
= the compounded amount, principal and interest, or accumulated value-the Sum
P
= the original principal amount or present value of S
i
= the rate of interest per period
n
= the number of conversion periods in the term or periods in which the
principal is compounded.
To illustrate this formula, suppose you
deposit $100 in a savings account paying 6% interest compounded quarterly. In
this case,
S=compounded
sum being sought
P=$100
i
= 1 1/2% or .0150 (the interest per period, the rate being 6% per year divide 6%
by 4 to get the quarterly rate)
n
= 4 (the number of conversion periods in the problem)
S
= P (1 + i)n
S
= 100 (1 + . 0150)4
S
= 100 (1.0150) (1.0150) (1.0150) (1.0150)
S
= 100 (1.0613634)
S
= $106.14
The total interest is $6.14 ($106.14-$100.00).By
solving for simple interest, the interest on $100 at 6% per annum is only $6.00.
Licensees should become well versed in
using these symbols, formulas and compound interest tables to be able to
calculate annuity payment values (mortgage payments, rents), sinking fund needs
(accumulation of money in equal periodic deposits at compound interest to meet
obligations, such as replacing depreciated assets or debt retirement) and
compute amortizations.
Effective Rate of Interest
he "nominal" or
"named" interest rate is that rate of interest stated in the loan
documents, while the effective interest rate is the rate the borrower is
actually paying, commonly called the annual percentage rate (APR).In other
words the loan papers may say one thing but the result is another, depending
upon how many times a year the actual earnings rate is compounded. The
effective rate of interest = the annual rate which will produce the same
interest in a year as the nominal rate converted a certain number of times. For
example, 6% converted semi-annually produces $6.09 per $100; therefore, 6% is
the nominal rate and 6.09% is the effective rate. A rate of 6% converted
semi-annually yields the same interest as a rate of 6.09% on an annual basis.
When the loan proceeds disbursed by the
lender are less than face value (the original principal sum stated in the
promissory note), the lender has deducted "up front" a loan fee and
perhaps discount points as compensation or remuneration for making the loan on
the agreed terms. The borrower thus receives less than must be repaid under the
contract. This lending practice is called "discounting. " Sometimes
under a bank's commercial loan terms the total interest is deducted in advance
from the principal amount of the loan before the loan proceeds are given to the
borrower. This method is usually associated with short-term bank loans, but
real estate lenders also discount loans by collecting "points" in
advance to increase yield.
When more accurate yield and interest
tables are unavailable, it is possible to approximate effective interest cost
to borrowers or a yield rate to a lender by using the following formulas where
discounted loans are involved:
i = approximate effective interest rate
(expressed as a decimal)
r = contract interest rate (expressed as
a decimal)
d = discount rate, or points deducted
(expressed as a decimal)
P
= principal
of loan (expressed as the whole number 1 for all dollar amounts)
n = term (years, periods, or fraction
thereof)
The formula for approximating the
effective rate of interest on a discounted real estate loan may be written:
i = r + (d/n)/(P-d)
Example:
What is the estimated approximate
effective interest on a $60,000 mortgage loan, with a 20 year term, contract
rate of interest being 12% per annum, discounted 3%, so that only $58,200 is
disbursed to the borrower?
i
= .12 + (.03/20)/(1-.03) = .12 + (.0015)/.97 = .121546 or 12.15%
Where published yield tables are
available, both the tables and the above formula should be compared, especially
when tables do not have fractional interest rates or uncommon terms. By
interpolation, errors in approximating the result can be minimized.
Principal-Plus-Interest. Another manner
of figuring interest is the Principal-Plus-Interest or the "interest
extra" approach. Here the borrower makes a fixed payment on the principal
each time plus paying the interest on the unpaid balance. Since the interest is
different each time, the total payment is different each time. This method is
not widely used in California in the case of first mortgages or trust deeds. It
is occasionally found in the case of secondary financing.
Straight Loan. This is an arrangement
where the principal of the loan is paid off in one lump sum rather than
periodic payments. This lump sum payment is usually made when the loan becomes
finally due. It is normal, however, that the interest payments be made at
intervals during the term of the loan.
Extended Term Amortization. Often in
commercial and industrial real estate loans with a very stable and secure
tenant the amortization payments are based on a payment schedule that is longer
than the actual term of the loan.
For example, the actual term of the loan
may be 25 years, but the monthly amortization payments may be based on a term
of 30 years. Obviously when the term of the loan ends there will be a balance
to be paid off in a lump sum or "balloon payment."
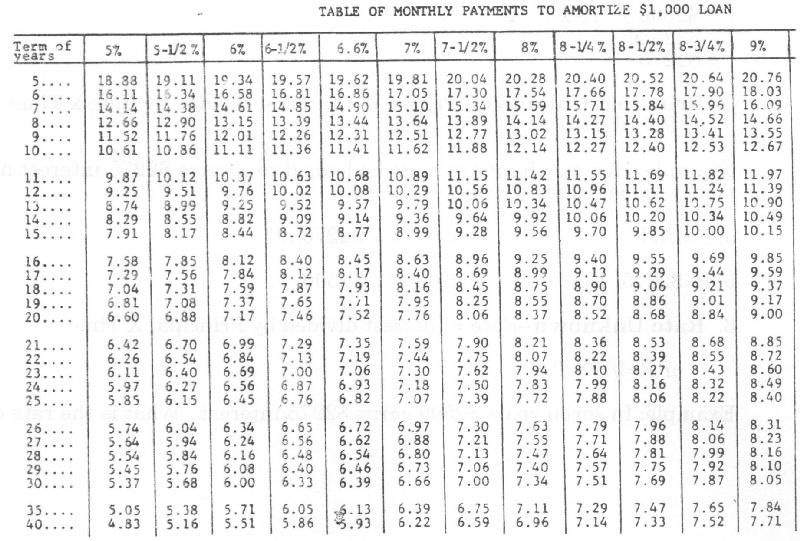
Computers Tables Formulas. The
mathematics of financing is generally done with appropriate mortgage tables and
formulas and with the computations completed by hand-held high-speed
calculators.
Courses in instruction in the use of
calculators, computers and the sophisticated tables and formulas in general use
are available in most communities.
There are some expenses connected with
owning real estate that are commonly paid for in arrears or in advance. For
example, fire insurance premiums are normally paid for in advance. Landlords
usually collect rents in advance, too. On the other hand, mortgage interest
accrues in arrears. Taxes, however, may be paid in advance or in arrears,
depending on the time of year of sale. Real property tax adjustment (proration)
depends on a number of things, such as: date current installation of taxes is
due? What portion of year's taxes has seller paid, is the escrow closing at a
time of year when current tax bill has not yet been issued by the tax
collector, and, if so, should the parties consider the possibility that the tax
bill will substantially increase over the preceding year and agree to a further
adjustment between themselves when the new tax bill is available?
When a property is sold, a portion of
these expenses has usually been used up by the seller and are rightfully an
expense of the seller. However, often a portion of the expenses of ownership
has not been used up and when the title to the property is passed on to the
buyer, the benefit of these advances will accrue to the buyer. It is only fair
that the buyer, therefore, reimburse the seller for the unused portions of
these expenses of homeownership.
These adjustments are normally made by
the process of proration. This simply means apportioning the expenses (or
benefits) fairly to each party.
For example, if the seller sells the
property six months after paying the annual fire insurance premium, 1/2 has not
been used up and will accrue to the benefit of the buyer. In this case, the
buyer should pay 1/2 of the insurance premium to the seller. This example is
over-simplified, of course. In practice, prorations are figured down to the day
with the so called Banker's rule of 30 days to a month and 360 days to a year
usually applying.
Taxes. The real property tax year runs
from July 1 of one year to June 30 of the following year (fiscal year).Taxes may
be paid in one or two installments. The first installment is due November 1.
The second is due February 1.The entire bill may be paid at the time the first
installment is due. Suppose an escrow for the sale of a small residence closed
January 16.Taxes for the full year in the amount of $600 are to be prorated as
of close of escrow between buyer and seller. How much should the buyer be
charged in escrow to reimburse the seller for advance paid taxes?
Taxes are paid through June 30th.Buyer
will owe seller for 5 1/2 months tax adjustment.$600/12 = $50/month.5 1/2 x 50
= $275 due seller.
Insurance. Fire insurance rates are
usually quoted at so much per $100 of coverage per year. Assume the rate is 95
cents per $100. For a $47,000 insurance policy paid in advance to March 31,
what will be the buyer's reimbursement to seller in the above escrow if the
insurance premium is an annual premium and adjustment is as of close of escrow?
Premium = $. 95 x 470 = $446. 50
Remaining days under policy = 75 days
$446.50/360 days = $1.24/day
$1.24 x 75 = $93 due seller.
Rents. Suppose the seller of a
single-family dwelling rented it for $450 a month. Rent was to be adjusted in
escrow as of the closing date of May 1.Rent is paid on the 25th of each month,
and the tenant is current in paying rent. Who is to be charged and credited in
the escrow on the rent adjustment? What is the amount of the adjustment?
Rents are paid in advance. Seller has
collected rents to May 25. Escrow will debit seller and credit buyer as follows:
$450/.30 = $15/day
24 (days of the adjustment) x $15 = $360
credit to buyer.
Mortgage
Interest. The buyer is purchasing a home subject to two assumable trust deeds
of record. Interest is to be prorated between buyer and seller as of close of escrow.
Both loans are current. Escrow closes on the 21st day of the month. The first
trust deed has an unpaid principal balance of $59,200, monthly installment
payments are $711. 54 including interest at 11. 5%. Payments are due the first
of each month. The second trust deed unpaid principal is $11,700, principal and
interest monthly payments are $200 per month, interest is 13% per annum,
monthly installments are due the 24th day of each month. Whose account is
credited for interest in the escrow?
First
trust deed Second
trust deed
51
21
days 21
days (closing
(closing
date) date)
-1
day -24
days
(interest
due date) (interest
due date
20
days of 27
days of
interest
owed interest
owed
by
seller by
seller
$59,200
x .115/360 $11,700
x .13/360xx 20 = $378.22, 27
= $114.08,
credit
buyer and credit
buyer and
debit
seller. debit
seller.
Taxes
and Assessments. As of June 1978 a limit on real property taxation was set by
constitutional amendment. This limitation is one percent of "full cash value"
(market value) plus a maximum authorized two percent annual inflationary factor
and an additional sum (averaging 1/5 to 1/4 of one percent) to pay for any
existing indebtedness on affected property, approved by voters prior to the
passage of the amendment.
In computing the tax to be paid on California
real property for the 1978-79 and subsequent Assessment Roll years, the
following is to be considered:
(1) the "full cash value" of the
property established as of (a) the lien date of the 1975 base year, or (b) the
date a property is purchased, newly constructed, or has a change of ownership,
after the 1975 lien date; (2) the maximum two percent inflationary factor
applied to the base value, which inflationary (cost of living) factor is to be
added to the base year value for each lien date after the lien date on which
"full cash value" is determined; (3) an additional amount may be
added to pay for any bonded indebtedness previously approved by the voters,
which amount will vary from county to county and will not be applicable to all
parcels.
For example, a county tax bill may be computed
as follows: assume an appraised value of $57,000; deduct homeowner's exemption
of $7,000, leaving $50,000 as amount taxable; multiply that amount by the tax
rate of .012 (1% tax limit plus two-tenths of one percent allowed for bonded
indebtedness); the resulting tax bill is $600. 00.
Because real property is reassessed as a result
of incidents of transfer (unless the transfer is subject to a statutory
exemption), a supplemental tax assessment is usually imposed by the county assessor.
This supplemental assessment increases the taxes due for the remainder of the
fiscal year within which the transfer occurred.
(End of the CalBRE Reference Book excerpt)